Advanced Technology Consultants
A Superior Source of Knowledge

Feyman lecture

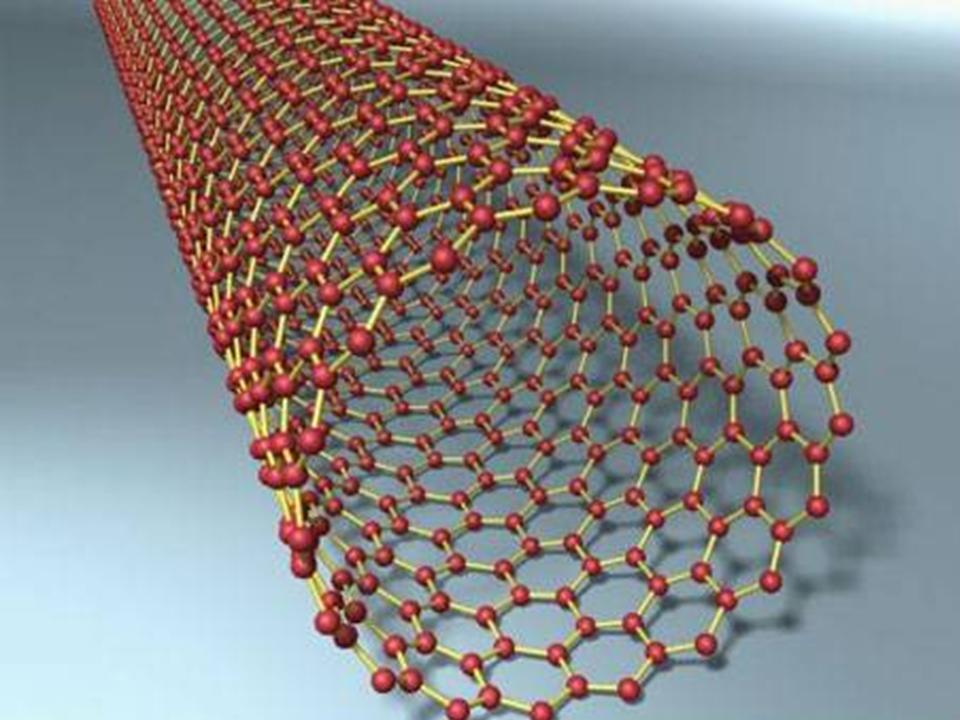There's Plenty of Room at the Bottom

  by Richard P. Feynman

Classic talk by Richard Feynman given on December 29th 1959 (American Physical Society at the California Institute of Technology (Caltech)  )

Information on the Feynman Prizes

Links to pages on Feynman

How people reacted to Feynman talk? See chapter 4 of Nano! by Ed Regis, Little/Brown 1995. 

For introduction to nanotechnology see  Nanosystems: molecular machinery, manufacturing, and computation by K. Eric Drexler, Wiley 1992.

**Other contributions of Feynman and his timeline**

I imagine experimental physicists must often look with envy at men like Kamerlingh Onnes, who discovered a field like low temperature, which seems to be bottomless and in which one can go down and down. Such a man is then a leader and has some temporary monopoly in a scientific adventure. Percy Bridgman, in designing a way to obtain higher pressures, opened up another new field and was able to move into it and to lead us all along. The development of ever higher vacuum was a continuing development of the same kind.

I would like to describe a field, in which little has been done, but in which an enormous amount can be done in principle. This field is not quite the same as the others in that it will not tell us much of fundamental physics (in the sense of, ``What are the strange particles?'') but it is more like solid-state physics in the sense that it might tell us much of great interest about the strange phenomena that occur in complex situations. Furthermore, a point that is most important is that it would have an enormous number of technical applications.

What I want to talk about is the problem of manipulating and controlling things on a small scale.

As soon as I mention this, people tell me about miniaturization, and how far it has progressed today. They tell me about electric motors that are the size of the nail on your small finger. And there is a device on the market, they tell me, by which you can write the Lord's Prayer on the head of a pin. But that's nothing; that's the most primitive, halting step in the direction I intend to discuss. It is a staggeringly small world that is below. In the year 2000, when they look back at this age, they will wonder why it was not until the year 1960 that anybody began seriously to move in this direction.

Why cannot we write the entire 24 volumes of the Encyclopedia Brittanica on the head of a pin?

Let's see what would be involved. The head of a pin is a sixteenth of an inch across. If you magnify it by 25,000 diameters, the area of the head of the pin is then equal to the area of all the pages of the Encyclopaedia Brittanica. Therefore, all it is necessary to do is to reduce in size all the writing in the Encyclopaedia by 25,000 times. Is that possible? The resolving power of the eye is about 1/120 of an inch---that is roughly the diameter of one of the little dots on the fine half-tone reproductions in the Encyclopaedia. This, when you demagnify it by 25,000 times, is still 80 angstroms in diameter---32 atoms across, in an ordinary metal. In other words, one of those dots still would contain in its area 1,000 atoms. So, each dot can easily be adjusted in size as required by the photoengraving, and there is no question that there is enough room on the head of a pin to put all of the Encyclopaedia Brittanica.

Furthermore, it can be read if it is so written. Let's imagine that it is written in raised letters of metal; that is, where the black is in the Encyclopedia, we have raised letters of metal that are actually 1/25,000 of their ordinary size. How would we read it?

If we had something written in such a way, we could read it using techniques in common use today. (They will undoubtedly find a better way when we do actually have it written, but to make my point conservatively I shall just take techniques we know today.) We would press the metal into a plastic material and make a mold of it, then peel the plastic off very carefully, evaporate silica into the plastic to get a very thin film, then shadow it by evaporating gold at an angle against the silica so that all the little letters will appear clearly, dissolve the plastic away from the silica film, and then look through it with an electron microscope!

There is no question that if the thing were reduced by 25,000 times in the form of raised letters on the pin, it would be easy for us to read it today. Furthermore; there is no question that we would find it easy to make copies of the master; we would just need to press the same metal plate again into plastic and we would have another copy.

How do we write small?

This method might be very slow because of space charge limitations. There will be more rapid methods. We could first make, perhaps by some photo process, a screen which has holes in it in the form of the letters. Then we would strike an arc behind the holes and draw metallic ions through the holes; then we could again use our system of lenses and make a small image in the form of ions, which would deposit the metal on the pin.

A simpler way might be this (though I am not sure it would work): We take light and, through an optical microscope running backwards, we focus it onto a very small photoelectric screen. Then electrons come away from the screen where the light is shining. These electrons are focused down in size by the electron microscope lenses to impinge directly upon the surface of the metal. Will such a beam etch away the metal if it is run long enough? I don't know. If it doesn't work for a metal surface, it must be possible to find some surface with which to coat the original pin so that, where the electrons bombard, a change is made which we could recognize later.

There is no intensity problem in these devices---not what you are used to in magnification, where you have to take a few electrons and spread them over a bigger and bigger screen; it is just the opposite. The light which we get from a page is concentrated onto a very small area so it is very intense. The few electrons which come from the photoelectric screen are demagnified down to a very tiny area so that, again, they are very intense. I don't know why this hasn't been done yet!

That's the Encyclopaedia Brittanica on the head of a pin, but let's consider all the books in the world. The Library of Congress has approximately 9 million volumes; the British Museum Library has 5 million volumes; there are also 5 million volumes in the National Library in France. Undoubtedly there are duplications, so let us say that there are some 24 million volumes of interest in the world.

What would happen if I print all this down at the scale we have been discussing? How much space would it take? It would take, of course, the area of about a million pinheads because, instead of there being just the 24 volumes of the Encyclopaedia, there are 24 million volumes. The million pinheads can be put in a square of a thousand pins on a side, or an area of about 3 square yards. That is to say, the silica replica with the paper-thin backing of plastic, with which we have made the copies, with all this information, is on an area of approximately the size of 35 pages of the Encyclopaedia. That is about half as many pages as there are in this magazine. All of the information which all of mankind has every recorded in books can be carried around in a pamphlet in your hand---and not written in code, but a simple reproduction of the original pictures, engravings, and everything else on a small scale without loss of resolution.

What would our librarian at Caltech say, as she runs all over from one building to another, if I tell her that, ten years from now, all of the information that she is struggling to keep track of--- 120,000 volumes, stacked from the floor to the ceiling, drawers full of cards, storage rooms full of the older books---can be kept on just one library card! When the University of Brazil, for example, finds that their library is burned, we can send them a copy of every book in our library by striking off a copy from the master plate in a few hours and mailing it in an envelope no bigger or heavier than any other ordinary air mail letter.

Now, the name of this talk is ``There is Plenty of Room at the Bottom''---not just ``There is Room at the Bottom.'' What I have demonstrated is that there is room---that you can decrease the size of things in a practical way. I now want to show that there is plenty of room. I will not now discuss how we are going to do it, but only what is possible in principle---in other words, what is possible according to the laws of physics. I am not inventing anti-gravity, which is possible someday only if the laws are not what we think. I am telling you what could be done if the laws are what we think; we are not doing it simply because we haven't yet gotten around to it.

Information on a small scale

Let us represent a dot by a small spot of one metal, the next dash, by an adjacent spot of another metal, and so on. Suppose, to be conservative, that a bit of information is going to require a little cube of atoms 5 times 5 times 5---that is 125 atoms. Perhaps we need a hundred and some odd atoms to make sure that the information is not lost through diffusion, or through some other process.

I have estimated how many letters there are in the Encyclopaedia, and I have assumed that each of my 24 million books is as big as an Encyclopaedia volume, and have calculated, then, how many bits of information there are (10^15). For each bit I allow 100 atoms. And it turns out that all of the information that man has carefully accumulated in all the books in the world can be written in this form in a cube of material one two-hundredth of an inch wide--- which is the barest piece of dust that can be made out by the human eye. So there is plenty of room at the bottom! Don't tell me about microfilm!

This fact---that enormous amounts of information can be carried in an exceedingly small space---is, of course, well known to the biologists, and resolves the mystery which existed before we understood all this clearly, of how it could be that, in the tiniest cell, all of the information for the organization of a complex creature such as ourselves can be stored. All this information---whether we have brown eyes, or whether we think at all, or that in the embryo the jawbone should first develop with a little hole in the side so that later a nerve can grow through it---all this information is contained in a very tiny fraction of the cell in the form of long-chain DNA molecules in which approximately 50 atoms are used for one bit of information about the cell.

Better electron microscopes

We have friends in other fields---in biology, for instance. We physicists often look at them and say, ``You know the reason you fellows are making so little progress?'' (Actually I don't know any field where they are making more rapid progress than they are in biology today.) ``You should use more mathematics, like we do.'' They could answer us---but they're polite, so I'll answer for them: ``What you should do in order for us to make more rapid progress is to make the electron microscope 100 times better.''

What are the most central and fundamental problems of biology today? They are questions like: What is the sequence of bases in the DNA? What happens when you have a mutation? How is the base order in the DNA connected to the order of amino acids in the protein? What is the structure of the RNA; is it single-chain or double-chain, and how is it related in its order of bases to the DNA? What is the organization of the microsomes? How are proteins synthesized? Where does the RNA go? How does it sit? Where do the proteins sit? Where do the amino acids go in? In photosynthesis, where is the chlorophyll; how is it arranged; where are the carotenoids involved in this thing? What is the system of the conversion of light into chemical energy?

It is very easy to answer many of these fundamental biological questions; you just look at the thing! You will see the order of bases in the chain; you will see the structure of the microsome. Unfortunately, the present microscope sees at a scale which is just a bit too crude. Make the microscope one hundred times more powerful, and many problems of biology would be made very much easier. I exaggerate, of course, but the biologists would surely be very thankful to you---and they would prefer that to the criticism that they should use more mathematics.

The theory of chemical processes today is based on theoretical physics. In this sense, physics supplies the foundation of chemistry. But chemistry also has analysis. If you have a strange substance and you want to know what it is, you go through a long and complicated process of chemical analysis. You can analyze almost anything today, so I am a little late with my idea. But if the physicists wanted to, they could also dig under the chemists in the problem of chemical analysis. It would be very easy to make an analysis of any complicated chemical substance; all one would have to do would be to look at it and see where the atoms are. The only trouble is that the electron microscope is one hundred times too poor. (Later, I would like to ask the question: Can the physicists do something about the third problem of chemistry---namely, synthesis? Is there a physical way to synthesize any chemical substance?

The reason the electron microscope is so poor is that the f- value of the lenses is only 1 part to 1,000; you don't have a big enough numerical aperture. And I know that there are theorems which prove that it is impossible, with axially symmetrical stationary field lenses, to produce an f-value any bigger than so and so; and therefore the resolving power at the present time is at its theoretical maximum. But in every theorem there are assumptions. Why must the field be symmetrical? I put this out as a challenge: Is there no way to make the electron microscope more powerful?

The marvelous biological system

There may even be an economic point to this business of making things very small. Let me remind you of some of the problems of computing machines. In computers we have to store an enormous amount of information. The kind of writing that I was mentioning before, in which I had everything down as a distribution of metal, is permanent. Much more interesting to a computer is a way of writing, erasing, and writing something else. (This is usually because we don't want to waste the material on which we have just written. Yet if we could write it in a very small space, it wouldn't make any difference; it could just be thrown away after it was read. It doesn't cost very much for the material).

Miniaturizing the computer

If I look at your face I immediately recognize that I have seen it before. (Actually, my friends will say I have chosen an unfortunate example here for the subject of this illustration. At least I recognize that it is a man and not an apple.) Yet there is no machine which, with that speed, can take a picture of a face and say even that it is a man; and much less that it is the same man that you showed it before---unless it is exactly the same picture. If the face is changed; if I am closer to the face; if I am further from the face; if the light changes---I recognize it anyway. Now, this little computer I carry in my head is easily able to do that. The computers that we build are not able to do that. The number of elements in this bone box of mine are enormously greater than the number of elements in our ``wonderful'' computers. But our mechanical computers are too big; the elements in this box are microscopic. I want to make some that are submicroscopic.

If we wanted to make a computer that had all these marvelous extra qualitative abilities, we would have to make it, perhaps, the size of the Pentagon. This has several disadvantages. First, it requires too much material; there may not be enough germanium in the world for all the transistors which would have to be put into this enormous thing. There is also the problem of heat generation and power consumption; TVA would be needed to run the computer. But an even more practical difficulty is that the computer would be limited to a certain speed. Because of its large size, there is finite time required to get the information from one place to another. The information cannot go any faster than the speed of light---so, ultimately, when our computers get faster and faster and more and more elaborate, we will have to make them smaller and smaller.

But there is plenty of room to make them smaller. There is nothing that I can see in the physical laws that says the computer elements cannot be made enormously smaller than they are now. In fact, there may be certain advantages.

Miniaturization by evaporation

But I would like to discuss, just for amusement, that there are other possibilities. Why can't we manufacture these small computers somewhat like we manufacture the big ones? Why can't we drill holes, cut things, solder things, stamp things out, mold different shapes all at an infinitesimal level? What are the limitations as to how small a thing has to be before you can no longer mold it? How many times when you are working on something frustratingly tiny like your wife's wrist watch, have you said to yourself, ``If I could only train an ant to do this!'' What I would like to suggest is the possibility of training an ant to train a mite to do this. What are the possibilities of small but movable machines? They may or may not be useful, but they surely would be fun to make.

Consider any machine---for example, an automobile---and ask about the problems of making an infinitesimal machine like it. Suppose, in the particular design of the automobile, we need a certain precision of the parts; we need an accuracy, let's suppose, of 4/10,000 of an inch. If things are more inaccurate than that in the shape of the cylinder and so on, it isn't going to work very well. If I make the thing too small, I have to worry about the size of the atoms; I can't make a circle of ``balls'' so to speak, if the circle is too small. So, if I make the error, corresponding to 4/10,000 of an inch, correspond to an error of 10 atoms, it turns out that I can reduce the dimensions of an automobile 4,000 times, approximately---so that it is 1 mm. across. Obviously, if you redesign the car so that it would work with a much larger tolerance, which is not at all impossible, then you could make a much smaller device.

It is interesting to consider what the problems are in such small machines. Firstly, with parts stressed to the same degree, the forces go as the area you are reducing, so that things like weight and inertia are of relatively no importance. The strength of material, in other words, is very much greater in proportion. The stresses and expansion of the flywheel from centrifugal force, for example, would be the same proportion only if the rotational speed is increased in the same proportion as we decrease the size. On the other hand, the metals that we use have a grain structure, and this would be very annoying at small scale because the material is not homogeneous. Plastics and glass and things of this amorphous nature are very much more homogeneous, and so we would have to make our machines out of such materials.

There are problems associated with the electrical part of the system---with the copper wires and the magnetic parts. The magnetic properties on a very small scale are not the same as on a large scale; there is the ``domain'' problem involved. A big magnet made of millions of domains can only be made on a small scale with one domain. The electrical equipment won't simply be scaled down; it has to be redesigned. But I can see no reason why it can't be redesigned to work again.

Problems of lubrication

This rapid heat loss would prevent the gasoline from exploding, so an internal combustion engine is impossible. Other chemical reactions, liberating energy when cold, can be used. Probably an external supply of electrical power would be most convenient for such small machines.

What would be the utility of such machines? Who knows? Of course, a small automobile would only be useful for the mites to drive around in, and I suppose our Christian interests don't go that far. However, we did note the possibility of the manufacture of small elements for computers in completely automatic factories, containing lathes and other machine tools at the very small level. The small lathe would not have to be exactly like our big lathe. I leave to your imagination the improvement of the design to take full advantage of the properties of things on a small scale, and in such a way that the fully automatic aspect would be easiest to manage.

A friend of mine (Albert R. Hibbs) suggests a very interesting possibility for relatively small machines. He says that, although it is a very wild idea, it would be interesting in surgery if you could swallow the surgeon. You put the mechanical surgeon inside the blood vessel and it goes into the heart and ``looks'' around. (Of course the information has to be fed out.) It finds out which valve is the faulty one and takes a little knife and slices it out. Other small machines might be permanently incorporated in the body to assist some inadequately-functioning organ.

Now comes the interesting question: How do we make such a tiny mechanism? I leave that to you. However, let me suggest one weird possibility. You know, in the atomic energy plants they have materials and machines that they can't handle directly because they have become radioactive. To unscrew nuts and put on bolts and so on, they have a set of master and slave hands, so that by operating a set of levers here, you control the ``hands'' there, and can turn them this way and that so you can handle things quite nicely.

Most of these devices are actually made rather simply, in that there is a particular cable, like a marionette string, that goes directly from the controls to the ``hands.'' But, of course, things also have been made using servo motors, so that the connection between the one thing and the other is electrical rather than mechanical. When you turn the levers, they turn a servo motor, and it changes the electrical currents in the wires, which repositions a motor at the other end.

Now, I want to build much the same device---a master-slave system which operates electrically. But I want the slaves to be made especially carefully by modern large-scale machinists so that they are one-fourth the scale of the ``hands'' that you ordinarily maneuver. So you have a scheme by which you can do things at one- quarter scale anyway---the little servo motors with little hands play with little nuts and bolts; they drill little holes; they are four times smaller. Aha! So I manufacture a quarter-size lathe; I manufacture quarter-size tools; and I make, at the one-quarter scale, still another set of hands again relatively one-quarter size! This is one-sixteenth size, from my point of view. And after I finish doing this I wire directly from my large-scale system, through transformers perhaps, to the one-sixteenth-size servo motors. Thus I can now manipulate the one-sixteenth size hands.

Well, you get the principle from there on. It is rather a difficult program, but it is a possibility. You might say that one can go much farther in one step than from one to four. Of course, this has all to be designed very carefully and it is not necessary simply to make it like hands. If you thought of it very carefully, you could probably arrive at a much better system for doing such things.

If you work through a pantograph, even today, you can get much more than a factor of four in even one step. But you can't work directly through a pantograph which makes a smaller pantograph which then makes a smaller pantograph---because of the looseness of the holes and the irregularities of construction. The end of the pantograph wiggles with a relatively greater irregularity than the irregularity with which you move your hands. In going down this scale, I would find the end of the pantograph on the end of the pantograph on the end of the pantograph shaking so badly that it wasn't doing anything sensible at all.

At each stage, it is necessary to improve the precision of the apparatus. If, for instance, having made a small lathe with a pantograph, we find its lead screw irregular---more irregular than the large-scale one---we could lap the lead screw against breakable nuts that you can reverse in the usual way back and forth until this lead screw is, at its scale, as accurate as our original lead screws, at our scale.

We can make flats by rubbing unflat surfaces in triplicates together---in three pairs---and the flats then become flatter than the thing you started with. Thus, it is not impossible to improve precision on a small scale by the correct operations. So, when we build this stuff, it is necessary at each step to improve the accuracy of the equipment by working for awhile down there, making accurate lead screws, Johansen blocks, and all the other materials which we use in accurate machine work at the higher level. We have to stop at each level and manufacture all the stuff to go to the next level---a very long and very difficult program. Perhaps you can figure a better way than that to get down to small scale more rapidly.

Yet, after all this, you have just got one little baby lathe four thousand times smaller than usual. But we were thinking of making an enormous computer, which we were going to build by drilling holes on this lathe to make little washers for the computer. How many washers can you manufacture on this one lathe?

A hundred tiny hands

Where am I going to put the million lathes that I am going to have? Why, there is nothing to it; the volume is much less than that of even one full-scale lathe. For instance, if I made a billion little lathes, each 1/4000 of the scale of a regular lathe, there are plenty of materials and space available because in the billion little ones there is less than 2 percent of the materials in one big lathe.

It doesn't cost anything for materials, you see. So I want to build a billion tiny factories, models of each other, which are manufacturing simultaneously, drilling holes, stamping parts, and so on.

As we go down in size, there are a number of interesting problems that arise. All things do not simply scale down in proportion. There is the problem that materials stick together by the molecular (Van der Waals) attractions. It would be like this: After you have made a part and you unscrew the nut from a bolt, it isn't going to fall down because the gravity isn't appreciable; it would even be hard to get it off the bolt. It would be like those old movies of a man with his hands full of molasses, trying to get rid of a glass of water. There will be several problems of this nature that we will have to be ready to design for.

Rearranging the atoms

Up to now, we have been content to dig in the ground to find minerals. We heat them and we do things on a large scale with them, and we hope to get a pure substance with just so much impurity, and so on. But we must always accept some atomic arrangement that nature gives us. We haven't got anything, say, with a ``checkerboard'' arrangement, with the impurity atoms exactly arranged 1,000 angstroms apart, or in some other particular pattern.

What could we do with layered structures with just the right layers? What would the properties of materials be if we could really arrange the atoms the way we want them? They would be very interesting to investigate theoretically. I can't see exactly what would happen, but I can hardly doubt that when we have some control of the arrangement of things on a small scale we will get an enormously greater range of possible properties that substances can have, and of different things that we can do.

Consider, for example, a piece of material in which we make little coils and condensers (or their solid state analogs) 1,000 or 10,000 angstroms in a circuit, one right next to the other, over a large area, with little antennas sticking out at the other end---a whole series of circuits. Is it possible, for example, to emit light from a whole set of antennas, like we emit radio waves from an organized set of antennas to beam the radio programs to Europe? The same thing would be to beam the light out in a definite direction with very high intensity. (Perhaps such a beam is not very useful technically or economically.)

I have thought about some of the problems of building electric circuits on a small scale, and the problem of resistance is serious. If you build a corresponding circuit on a small scale, its natural frequency goes up, since the wave length goes down as the scale; but the skin depth only decreases with the square root of the scale ratio, and so resistive problems are of increasing difficulty. Possibly we can beat resistance through the use of superconductivity if the frequency is not too high, or by other tricks.

Atoms in a small world

Another thing we will notice is that, if we go down far enough, all of our devices can be mass produced so that they are absolutely perfect copies of one another. We cannot build two large machines so that the dimensions are exactly the same. But if your machine is only 100 atoms high, you only have to get it correct to one-half of one percent to make sure the other machine is exactly the same size---namely, 100 atoms high!

At the atomic level, we have new kinds of forces and new kinds of possibilities, new kinds of effects. The problems of manufacture and reproduction of materials will be quite different. I am, as I said, inspired by the biological phenomena in which chemical forces are used in repetitious fashion to produce all kinds of weird effects (one of which is the author).

The principles of physics, as far as I can see, do not speak against the possibility of maneuvering things atom by atom. It is not an attempt to violate any laws; it is something, in principle, that can be done; but in practice, it has not been done because we are too big.

Ultimately, we can do chemical synthesis. A chemist comes to us and says, ``Look, I want a molecule that has the atoms arranged thus and so; make me that molecule.'' The chemist does a mysterious thing when he wants to make a molecule. He sees that it has got that ring, so he mixes this and that, and he shakes it, and he fiddles around. And, at the end of a difficult process, he usually does succeed in synthesizing what he wants. By the time I get my devices working, so that we can do it by physics, he will have figured out how to synthesize absolutely anything, so that this will really be useless.

But it is interesting that it would be, in principle, possible (I think) for a physicist to synthesize any chemical substance that the chemist writes down. Give the orders and the physicist synthesizes it. How? Put the atoms down where the chemist says, and so you make the substance. The problems of chemistry and biology can be greatly helped if our ability to see what we are doing, and to do things on an atomic level, is ultimately developed---a development which I think cannot be avoided.

Now, you might say, ``Who should do this and why should they do it?'' Well, I pointed out a few of the economic applications, but I know that the reason that you would do it might be just for fun. But have some fun! Let's have a competition between laboratories. Let one laboratory make a tiny motor which it sends to another lab which sends it back with a thing that fits inside the shaft of the first motor.

High school competition

Perhaps this doesn't excite you to do it, and only economics will do so. Then I want to do something; but I can't do it at the present moment, because I haven't prepared the ground. It is my intention to offer a prize of $1,000 to the first guy who can take the information on the page of a book and put it on an area 1/25,000 smaller in linear scale in such manner that it can be read by an electron microscope.

And I want to offer another prize---if I can figure out how to phrase it so that I don't get into a mess of arguments about definitions---of another $1,000 to the first guy who makes an operating electric motor---a rotating electric motor which can be controlled from the outside and, not counting the lead-in wires, is only 1/64 inch cube.

I do not expect that such prizes will have to wait very long for claimants.

Copyright 2017 - Advanced Technology Consultants- All Rights Reserved